位运算基础 计算机原码,反码,补码
一. 概念
1. 机器数
一个数在计算机中的表现形式叫做机器数,这个数有正负之分,在计算机中用一个数的最高位(符号位)用来表示它的正负,其中0 表示正数,1 表示负数。
例如:
正数 7,在计算机中用一个8位的二进制数来表示,是 00000111,
负数 -7,则用 10000111 表示,这里的 00000111 和 10000111 是机器数
2. 真数
计算机中的机器数对应的真实的值就是真数,对最高位(符号位)后面的二进制数转换成 10进制,并根据最高位来确定这个数的正负。
对于上面的 00000111 和 10000111 来说,对最高位后面的二进制数转换成10进制是7,在结合最高位的值,得出对应的真数 分别是 7 和 -7
3. 原码(是容易被人脑所理解的表达方式)
是最简单的机器数表示法。用最高位表示符号位,‘1’表示负号,‘0’表示正号。其他位存放该数的二进制的绝对值。
因为第一位是符号位,所以 8位二进制数的取值范围就是:[1111_1111 , 0111_1111] 即 [-127 , 127] ,
4. 反码
正数的反码是其原码本身
负数的反码是符号位保持不变,其余位取反。
例如:
1的原码是[0000_0001],它的反码是其本身[0000_0001],
-1的原码是[1000_0001],其反码是 [1111_1110]
5. 补码(反码+1)
正数的补码是其原码本身
负数的补码是在其反码的基础上+1
例如:
1的原码是[0000_0001],它的补码是其本身[0000_0001],
-1的补码是[1111_1111]
二. 计算机的加法
原码,反码,补码的引入是为了解决做减法的问题。计算机中的没法直接做减法的,它的减法是通过加法来实现的(因为计算机没有负数的概念)。减去一个数,可以看作加上这个数的相反数。
从硬件的角度上看,只有正数加负数才算减法。 正数与正数相加,负数与负数相加,其实都可以通过加法器直接相加得来。
所有的运算,都是在 不溢出 的情况下计算,溢出还说个卵!
1. 原码的问题
下图给出部份正负数数的二进制原码表示法

尝试 用原码 运算:
正常:0001+0010=0011 (1+2=3)OK
正常:0000+1000=1000 (+0+(-0)=-0)
异常:0001+1001=1010 (1+(-1)=-2)
我们可以看到,只用原码进行运算,其实正数之间的加法通常是不会出错的,因为它就是一个很简单的二进制加法。
而正数与负数相加,或负数与负数相加,就要引起莫名其妙的错误,这都是符号位引起的。于是反码来了。
2. 反码的问题
下图给出部分正负数的二进制数反码表示法
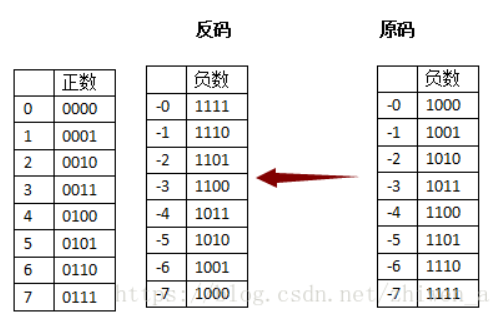
尝试 用反码 运算:
正常:0001(1) + 1110(-1)= 1111(-0)
异常:1110(-1)+ 1101(-2)= 1011(-4)
正常:0001(1)+1101(-2)=1110(-1)
反码的负数相加出错,其实问题不大。我们只需要加实现两个负数加法时,将两个负数反码包括符号位全部按位取反相加,然后再给他的符号位强行置‘1’就可以了。
反码与原码比较,最大的优点,就在于解决了减法的问题。
3. 补码
下图给出部分正负数的二进制数补码表示法
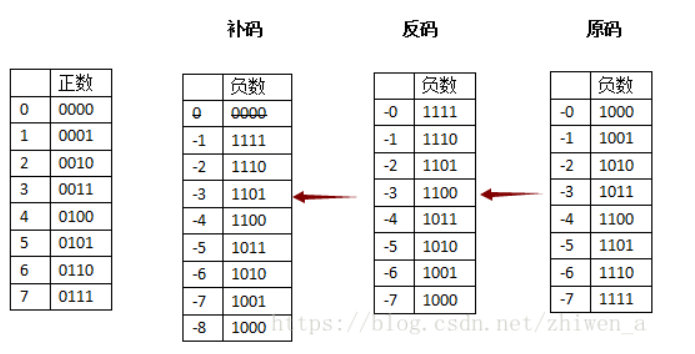
尝试 用补码 运算:
正常:0001(1)+1111(-1)=0000
正常:1111(-1)+1110(-2)=1101(-3)
到这里,我们发现原码,反码的问题,补码基本解决了。
在补码中也不存在负零了,因为1000表示-8
4. 为什么 负数的补码 是 反码+1
因为负数的反码加上这个负数的绝对值正好等于1111,再加1,就是1000,也就是四位二进数的模
而负数的补码是它的绝对值的同余数,可以通过模减去负数的绝对值,得到他的补码。
参考文档:
https://blog.csdn.net/chenchao2017/article/details/79733278
https://blog.csdn.net/afsvsv/article/details/94553228

共 0 条评论